
 |
| Home | Teacher | Parents | Glossary | About Us | |||||||||||
|
|
|||||||||||
|
|
In the previous lesson, you learned how to graph points on the coordinate plane. We can connect two points with a straight line.
To graph the equation of a line, we plot at least two points whose coordinates satisfy the equation, and then connect the points with a line. We call these equations "linear" because the graph of these equations is a straight line.
There are two important things that can help you graph an equation, slope and y-intercept.
Slope
We're familiar with the word "slope" as it relates to mountains.
Skiers and snowboarders refer to "hitting the slopes." On the coordinate
plane, the steepness, or slant, of a line is called the slope. Slope is the
ratio of the change in the y-value over the change in the x-value. Carpenters
and builders call this ratio the "rise over the run." Using any
two points on a line, you can calculate its slope using this formula.
![]()
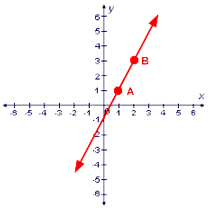
Let's use these
two points to calculate the slope m of this line.
A = (1,1) and B = (2,3)

Subtract the y value of point A from the y-value of point B to find the change in the y value, which is 2. Then subtract the x value of point A from the x value of point B to find the change in x, which is 1. The slope is 2 divided by 1, or 2.
![]()
When a line has positive slope, like this one, it rises from left to right.
 WATCH
OUT! Always use the same order in the numerator and denominator!
WATCH
OUT! Always use the same order in the numerator and denominator!
It doesn't really matter whether you subtract the values of point A from the values of point B, or the values of point B from the values of point A. Try it - you'll get the same answer both ways. But you must use the same order for both the numerator and denominator!
You can't subtract the y value of point A from the y value of point B, and the x value of point B from the x value of point A - your answer will be wrong.
Let's look at another line. This line has a negative slope, it falls from left to right. We can take any two points on this line and find the slope. Let's take C (0, -1) and D (2, -5).
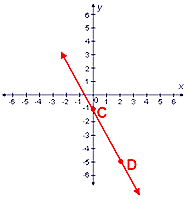
Using these two points, we can calculate the slope of this line. We subtract the y value of point C from the y value of point D, and the x value of point C from the x value of point D, and divide the first value by the second value. The slope is -2.
Y-Intercept
There's another important value associated with graphing a line on the coordinate
plane. It's called the "y intercept" and it's the y value of the
point where the line intersects the y- axis. For this line, the y-intercept
is "negative 1." You can find the y-intercept by looking at the
graph and seeing which point crosses the y axis. This point will always have
an x coordinate of zero. This is another way to find the y-intercept, if you
know the equation, the y-intercept is the solution to the equation when x
= 0.
Equations
Knowing how to find the slope and the y-intercept helps us to graph a line
when we know its equation, and also helps us to find the equation of a line
when we have its graph. The equation of a line can always be written in this
form, where m is the slope and b is the y-intercept:
y = mx + b
Let's find the equation for this line. Pick any two points, in this diagram, A = (1, 1) and B = (2, 3).
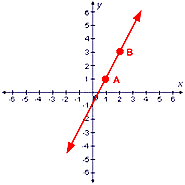
We found that the slope m for this line is 2. By looking at the graph, we can see that it intersects the y-axis at the point (0, –1), so –1 is the value of b, the y-intercept. Substituting these values into the equation formula, we get:
y = 2x –1
The line shows the solution to the equation: that is, it shows all the values that satisfy the equation. If we substitute the x and y values of a point on the line into the equation, you will get a true statement. We'll try it with the point (2, 3).
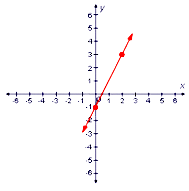
Let's substitute x = 2 and y = 3 into the equation. We get "3 = 3", a true statement, so this point satisfies the equation of the line.
| Homework Help | Algebra | Graphing Equations and Inequalities | |||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||