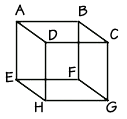
In geometry, lines often occur in pairs. We can define four different types of line pairs: lines that intersect, lines that are perpendicular, lines that are parallel, and lines that are skew. We can use this picture of a box to investigate each of these line pairs. Intersecting lines are lines that have one, and only one, point in common.

Look at the line segments formed by the edges of the box and find two line segments that intersect. There are several pairs of intersecting line segments—for example, line segment CG and line segment HG share one point in common, point G, so they are intersecting line segments.

Perpendicular lines intersect in a special way, forming right angles. You'll learn more about right angles in the next lesson. The x and y axes on the coordinate plane are a good example of perpendicular lines. This box has many perpendicular line segments. The intersecting line segments AE and EH are perpendicular, and so are the line segments CG and HG.

Parallel lines never touch, and they lie in the same plane. Can you find a pair of parallel lines on the box? Line segments AE and CG are parallel, and there are also several other sets of parallel edges.

Like parallel lines, skew lines never touch, but unlike parallel lines, skew lines are not in the same plane. Look at edge CG on the right front side of the box, going up and down, and edge AB at the back, going left to right. Do these lines ever touch each other? No, they don't. Are they in the same plane, meaning the same surface of the box? No, they are not. These segments are an example of skew lines.

back to top