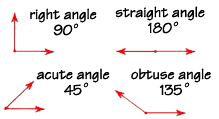
If you look around you, you'll see angles everywhere. Angles are measured in degrees. A degree is a fraction of a circle—there are 360 degrees in a circle, represented like this: 360°.

You can think of a right angle as one-fourth of a circle, which is 360° divided by 4, or 90°.

The right angle is the most common angle—the edges of your notebook paper, stair steps, door facings, the edges of picture frames—all of these form right angles. Let's look at some other types of angles. A straight angle represents half of a circle. 360° divided by 2 equals 180°—that is the measure of a straight angle. An acute angle is any angle that measures less than 90°. An obtuse angle measures greater than 90° but less than 180°.

We can estimate angle measures by looking at them and comparing them mentally with angles we know, such as the right angle. But how do we measure angles exactly?

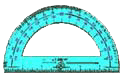
This useful tool is called a protractor, and any student of geometry should have one! It is used both to measure angles and to draw angles. To use a protractor, place the arrow on the vertex of the angle you want to measure, and read off the measurement on the scale, in degrees.

Two angles that have the same measure are called congruent angles.

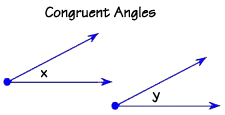
Here are two angles that both measure 30°. We say that angle x is congruent to angle y.

Now let's look at some angle pairs. Two angles are called supplementary if their measures add up to 180°. These two 90° angles are supplementary because 90 + 90 = 180.

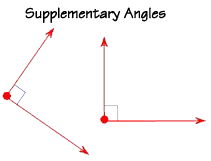
Supplementary angles do not have to touch, or be in the same plane, or even be in the same room! Their measurements only are the secret of their relationship!

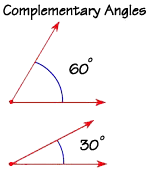
A pair of angles is called complementary if their measurements add up to 90°. These two angles are complementary, because 60 + 30 = 90.

back to top