|
Pi is a name given to the ratio of the circumference
of a circle to the diameter. That means, for any circle, you can divide
the circumference (the distance around the circle) by the diameter and
always get exactly the same number. It doesn't matter how big or small
the circle is, Pi remains the same. Pi is often written using the symbol
 and is pronounced
"pie", just like the dessert. and is pronounced
"pie", just like the dessert.
History | Pi
web sites| Do it yourself Pi
|The Digits| Formulas
A Brief History of Pi
Ancient civilizations knew that there was a fixed ratio of circumference
to diameter that was approximately equal to three. The Greeks refined
the process and Archimedes is credited with the first theoretical calculation
of Pi.
In 1761 Lambert proved that Pi was irrational, that is,
that it can't be written as a ratio of integer numbers.
In 1882 Lindeman proved that Pi was transcendental, that
is, that Pi is not the root of any algebraic equation with rational coefficients.
This discovery proved that you can't "square a circle", which
was a problem that occupied many mathematicians up to that time. (More
information on squaring
the circle.)
How many digits are there? Does it ever end?
Because Pi is known to be an irrational number it means that the digits
never end or repeat in any known way. But calculating the digits of Pi
has proven to be an fascination for mathematicians throughout history.
Some spent their lives calculating the digits of Pi, but until computers,
less than 1,000 digits had been calculated. In 1949, a computer calculated
2,000 digits and the race was on. Millions of digits have been calculated,
with the record held (as of September 1999) by a supercomputer at the
University of Tokyo that calculated 206,158,430,000 digits. (first
1,000 digits)
More about the History
of Pi can be found at the Mac Tutor Math History archives.
Approximation of Pi
Archimedes calculated that Pi was between 3 10/71 and 3 1/7
(also written 223/71 <  < 22/7 ). 22/7 is still a good approximation. 355/113 is a better one.
< 22/7 ). 22/7 is still a good approximation. 355/113 is a better one.
Pi Web Sites
Pi continues to be a fascination of many people around the world. If you
are interested in learning more, there are many web sites devoted to the
number Pi. There are sites that offer thousands, millions, or billions
of digits, pi clubs, pi music, people who calculate digits, people who
memorize digits, Pi experiments and more. Check this Yahoo
page for a complete listing.
A Cool Pi Experiment
One of the most interesting ways to learn more about Pi is to do pi experiments
yourself. Here is a famous one called Buffon's Needle.
In Buffon's Needle experiment you can drop a needle on
a lined sheet of paper. If you keep track of how many times the needle
lands on a line, it turns out to be directly related to the value of Pi.
Buffon's
Needle Simulation Applet (Michael J. Hurben)
Buffon's
Needle (George Reese, Office for Mathematics, Science and Technology
Education University of Illinois Champaign-Urbana)
Digits of Pi
First 100 decimal places
3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944
5923078164 0628620899 8628034825 3421170679 ...
First 1000 decimal places
3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164
0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172
5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975
6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482
1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436
7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953
0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381
8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277
0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342
7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235
4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837
2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035
2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904
2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787
6611195909 2164201989
5
million, 10 million, 100 million, and 200 million digits
Formulas for Pi
More complex
formulas and derivations
Vieta's Formula
2/PI = 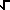 2/2
* 2/2
* 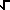 ( 2 + ( 2 + 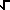 2
)/2 * 2
)/2 * 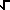 (2 + ( (2 + ( 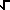 (
2 + (
2 + 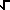 2) ) )/2 * ...c 2) ) )/2 * ...c
Leibnitz's Formula
PI/4 = 1/1 - 1/3 + 1/5 - 1/7 + ...
Wallis Product
PI/2 = 2/1 * 2/3 * 4/3 * 4/5 * 6/5 * 6/7 * ...
2/PI = (1 - 1/22)(1 - 1/42)(1 - 1/62)...
Lord Brouncker's Formula
4/PI = 1 + 1
----------------
2 + 32
------------
2 + 52
---------
2 + 72 ...
(PI2)/8 = 1/12 + 1/32 + 1/52
+ ...
(PI2)/24 = 1/22 + 1/42 + 1/62
+ ...
Euler's Formula
(PI2)/6 = 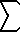 (n = 1..
(n = 1..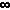 ) 1/n2 = 1/12
+ 1/22 + 1/32 + ... ) 1/n2 = 1/12
+ 1/22 + 1/32 + ...
(or more generally...)
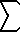 (n = 1.. (n = 1..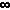 )
1/n(2k) = (-1)(k-1) PI(2k) 2(2k)
B(2k) / ( 2(2k)!) )
1/n(2k) = (-1)(k-1) PI(2k) 2(2k)
B(2k) / ( 2(2k)!)
B(k) = the k th Bernoulli number. eg. B0=1
B1=-1/2 B2=1/6 B4=-1/30 B6=1/42
B8=-1/30 B10=5/66. Further Bernoulli numbers are
defined as (n 0)B0 + (n 1)B1 + (n 2)B2
+ ... + (n (n-1))B(N-1) = 0 assuming all odd Bernoulli #'s
> 1 are = 0. (n k) = binomial coefficient = n!/(k!(n-k)!)
See Power Summations #2 for
simplified expressions (without the Bernoulli notation) of these sums
for given values of k.

|

