| Summation |
Expansion |
Equivalent Value |
Comments |
n
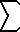 k k
k=1 |
= 1 + 2 + 3 + 4 + .. + n |
= (n2 + n) / 2
= (1/2)n2 + (1/2)n |
sum of 1st n integers |
n
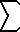 k 2 k 2
k=1 |
= 1 + 4 + 9 + 16 + .. + n2 |
= (1/6)n(n+1)(2n+1)
= (1/3)n3 + (1/2)n2 + (1/6)n |
sum of 1st n squares |
n
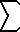 k 3 k 3
k=1 |
= 1 + 8 + 27 + 64 + .. + n3 |
= (1/4)n4 + (1/2)n3 + (1/4)n2 |
sum of 1st n cubes |
n
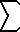 k 4 k 4
k=1 |
= 1 + 16 + 81 + 256 + .. + n4 |
= (1/5)n5 + (1/2)n4 + (1/3)n3 -
(1/30)n |
|
n
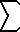 k 5 k 5
k=1 |
= 1 + 32 + 243 + 1024 + .. + n5 |
= (1/6)n6 + (1/2)n5 + (5/12)n4
- (1/12)n2 |
|
n
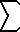 k 6 k 6
k=1 |
= 1 + 64 + 729 + 4096 + .. + n6 |
= (1/7)n7 + (1/2)n6 + (1/2)n5 -
(1/6)n3 + (1/42)n |
|
n
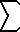 k 7 k 7
k=1 |
= 1 + 128 + 2187 + 16384 + .. + n7 |
= (1/8)n8 + (1/2)n7 + (7/12)n6
- (7/24)n4 + (1/12)n2 |
|
n
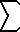 k 8 k 8
k=1 |
= 1 + 256 + 6561 + 65536 + .. + n8 |
= (1/9)n9 + (1/2)n8 + (2/3)n7 -
(7/15)n5 + (2/9)n3 - (1/30)n |
|
n
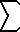 k 9 k 9
k=1 |
= 1 + 512 + 19683 + 262144 + .. + n9 |
= (1/10)n10 + (1/2)n9 + (3/4)n8
- (7/10)n6 + (1/2)n4 - (3/20)n2 |
|
n
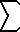 k 10 k 10
k=1 |
= 1 + 1024 + 59049 + 1048576 + .. + n10 |
= (1/11)n11 + (1/2)n10 + (5/6)n9
- n7 + n5 - (1/2)n3 + (5/66)n |
|

