|
|
|
Definition of Convergence and Divergence in Series
The nth partial sum of the series 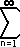 an is given by Sn = a1 + a2
+ a3 + ... + an. If the sequence of these partial
sums {Sn} converges to L, then the sum of the series converges
to L. If {Sn} diverges, then the sum of the series diverges.
an is given by Sn = a1 + a2
+ a3 + ... + an. If the sequence of these partial
sums {Sn} converges to L, then the sum of the series converges
to L. If {Sn} diverges, then the sum of the series diverges.
Operations on Convergent Series
If 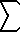 an
= A, and an
= A, and 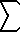 bn
= B, then the following also converge as indicated: bn
= B, then the following also converge as indicated:
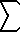 can = cA can = cA
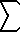 (an
+ bn) = A + B (an
+ bn) = A + B
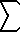 (an
- bn) = A - B (an
- bn) = A - B
Alphabetical Listing of Convergence Tests
Absolute Convergence
If the series 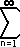 |an| converges, then the series
|an| converges, then the series 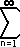 an also converges.
an also converges.
Alternating Series Test
If for all n, an is positive, non-increasing (i.e.
0 < an+1 <= an), and approaching zero, then
the alternating series
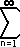 (-1)n
an and (-1)n
an and 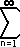 (-1)n-1 an
(-1)n-1 an
both converge.
If the alternating series converges, then the remainder RN
= S - SN (where S is the exact sum of the infinite series and
SN is the sum of the first N terms of the series) is bounded
by |RN| <= aN+1
Deleting the first N Terms
If N is a positive integer, then the series
both converge or both diverge.
Direct Comparison Test
If 0 <= an <= bn for all n greater
than some positive integer N, then the following rules apply:
If 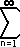 bn
converges, then bn
converges, then 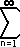 an converges.
an converges.
If 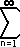 an
diverges, then an
diverges, then 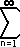 bn diverges.
bn diverges.
Geometric Series Convergence
The geometric series is given by
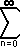 a rn = a + a r + a r2 + a r3 + ...
a rn = a + a r + a r2 + a r3 + ...
If |r| < 1 then the following geometric series converges to a / (1
- r).
If |r| >= 1 then the above geometric series diverges.
Integral Test
If for all n >= 1, f(n) = an, and f is positive,
continuous, and decreasing then
either both converge or both diverge.
If the above series converges, then the remainder RN = S -
SN (where S is the exact sum of the infinite series and SN
is the sum of the first N terms of the series) is bounded by 0< = RN
<= 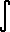 (N.. (N..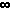 )
f(x) dx. )
f(x) dx.
Limit Comparison Test
If lim (n-->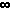 ) (an
/ bn) = L, ) (an
/ bn) = L,
where an, bn > 0 and L is finite and positive,
then the series 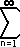 an and
an and 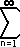 bn either both converge or both diverge.
bn either both converge or both diverge.
nth-Term Test for Divergence
If the sequence {an} does not converge to zero, then the series 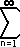 an diverges.
an diverges.
p-Series Convergence
The p-series is given by
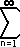 1/np
= 1/1p + 1/2p + 1/3p + ... 1/np
= 1/1p + 1/2p + 1/3p + ...
where p > 0 by definition.
If p > 1, then the series converges.
If 0 < p <= 1 then the series diverges.
Ratio Test
If for all n, n 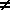 0, then the following rules apply:
0, then the following rules apply:
Let L = lim (n -- > 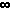 )
| an+1 / an |. )
| an+1 / an |.
If L < 1, then the series 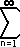 an converges.
an converges.
If L > 1, then the series 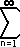 an diverges.
an diverges.
If L = 1, then the test in inconclusive.
Root Test
Let L = lim (n -- > 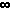 )
| an |1/n. )
| an |1/n.
If L < 1, then the series 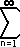 an converges.
an converges.
If L > 1, then the series 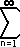 an diverges.
an diverges.
If L = 1, then the test in inconclusive.
Taylor Series Convergence
If f has derivatives of all orders in an interval I centered
at c, then the Taylor series converges as indicated:
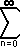 (1/n!)
f(n)(c) (x - c)n = f(x) (1/n!)
f(n)(c) (x - c)n = f(x)
if and only if lim (n-->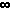 )
RN = 0 for all x in I. )
RN = 0 for all x in I.
The remainder RN = S - SN of the Taylor series (where
S is the exact sum of the infinite series and SN is the sum
of the first N terms of the series) is equal to (1/(n+1)!) f(n+1)(z)
(x - c)n+1, where z is some constant between x and c.
|
|
|

