|
|
|
|
Interest and Exponential
Growth |
|
(Math | General
| Interest and Exponential Growth) |
The Compound Interest Equation
P = C (1 + r/n) nt
where
P = future value
C = initial deposit
r = interest rate (expressed as a fraction: eg. 0.06)
n = # of times per year interest is compounded
t = number of years invested
Simplified Compound Interest Equation
When interest is only compounded once per year (n=1), the equation simplifies
to:
P = C (1 + r) t
Continuous Compound Interest
When interest is compounded continually (i.e. n -->  ),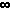
the compound interest equation takes the form:
P = C e rt
Demonstration of Various Compounding
The following table shows the final principal (P), after t = 1 year, of
an account initially with C = $10000, at 6% interest rate, with the given
compounding (n). As is shown, the method of compounding has little effect.
| n |
P |
| 1 (yearly) |
$ 10600.00 |
| 2 (semiannually) |
$ 10609.00 |
| 4 (quarterly) |
$ 10613.64 |
| 12 (monthly) |
$ 10616.78 |
| 52 (weekly) |
$ 10618.00 |
| 365 (daily) |
$ 10618.31 |
| continuous |
$ 10618.37 |
Loan Balance
Situation: A person initially borrows an amount A and
in return agrees to make n repayments per year, each of an amount
P. While the person is repaying the loan, interest is accumulating
at an annual percentage rate of r, and this interest is compounded
n times a year (along with each payment). Therefore, the person must continue
paying these installments of amount P until the original amount and
any accumulated interest is repaid. This equation gives the amount B
that the person still needs to repay after t years.
| B = A (1 + r/n)NT - P |
(1 + r/n)NT - 1
(1 + r/n) - 1
|
where
B = balance after t years
A = amount borrowed
n = number of payments per year
P = amount paid per payment
r = annual percentage rate (APR)
|
|
|
