un círculo

Definiciones respecto a círculos

un arco: una línea curva que es una parte de la circunferencia de un círculo. una cuerda: un segmento de línea que está en contacto con dos puntos del círculo. la circunferencia: la distancia alrededor de un círculo. el diámetro: la distancia mas larga desde un cabo de un círculo hacía el otro. el origin: el centro del círculo. pi (): Un número, 3.141592..., igual a (la circunferencia) / (el diámetro) de un círculo. el radio: la distancia desde el centro de un círculo hacía cualquier punto en él. un sector: es como una rebanada de pastel (una cuña de círculo). la tangente de un círculo: una línea, perpendicular al radio, que toca en solamente un punto al círculo.

La circunferencia del círculo = PI x diámetro = 2 PI x radio
    cuando PI = = 3.141592...

El área del círculo:
    el área = PI r²

El largo de un arco circular: (con ángulo central )
    si el ángulo está en grados, pues el largo = x (PI/180) x r
    si el ángulo está en radianes, pues el largo = r x

Área de un sector de círculo: (con ángulo central )
    si el ángulo está en grados, pues área = (/360)x PI r²
    si el ángulo está en radianes, pues área = (/2)x PI r²

La ecuación de un círculo: (coordenadas cartesianas)

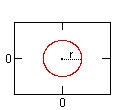
  para un círculo con centro (j, k) y radio (r):
    (x-j)² + (y-k)² = r²

Ecuación de un círculo: (coordenadas polares)
    para un círculo con centro (0, 0):   r() = radio

    para un círculo con centro con coordenadas polares: (c, ) y radio a:
      r² - 2cr cos( - ) + c² = a²

Ecuación de un círculo: (coordenadas paramétricas)
    para un círculo con origen (j, k) y radio r:
      x(t) = r cos(t) + j       y(t) = r sin(t) + k

 
Contact us | Advertising & Sponsorship | Partnership | Link to us

© 2000-2023 Math.com. All rights reserved.     Legal Notices.     Please read our Privacy Policy.