|
|
|

Algunas de estas funciones las he visto definidas en ambos intervalos (0
a x) y (x a inf). En ese caso, los dos varientes se dan.
gamma = la constante
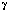 de Euler
= 0.5772156649... de Euler
= 0.5772156649...
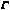 (x) = Gamma(x)
= (x) = Gamma(x)
=   t
(x-1) e -tdt (Función
gamma) t
(x-1) e -tdt (Función
gamma)
B(x,y) =   t
(x-1) (1-t) (y-1)dt (Función
beta) t
(x-1) (1-t) (y-1)dt (Función
beta)
Ei(x) =   e
-t/t dt (Integral exponencial) ó
una variente no eqivalente: e
-t/t dt (Integral exponencial) ó
una variente no eqivalente:
Ei(x) = 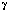 + ln(x) +
+ ln(x) +   (e
t - 1)/t dt = gamma + ln(x) + (e
t - 1)/t dt = gamma + ln(x) + 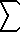 (n=1..inf)x
n/(n*n!) (n=1..inf)x
n/(n*n!)
li(x) =   1/ln(t)
dt (Integral del logaritmo) 1/ln(t)
dt (Integral del logaritmo)
Si(x) =   sen(t)/t
dt (Integral del seno) ó una variente
no eqivalente: sen(t)/t
dt (Integral del seno) ó una variente
no eqivalente:
Si(x) =   sen(t)/t
dt = PI/2 - sen(t)/t
dt = PI/2 -   sen(t)/t
dt sen(t)/t
dt
Ci(x) =   cos(t)/t
dt (Integral del coseno) ó una variente
no eqivalente: cos(t)/t
dt (Integral del coseno) ó una variente
no eqivalente:
Ci(x) = -   cos(t)/t
dt = gamma + ln(x) + cos(t)/t
dt = gamma + ln(x) +   (cos(t) - 1) / t dt
(cos(t) - 1) / t dt
Chi(x) = gamma + ln(x) +   (cosh(t)-1)/t
dt (Integral del coseno hiperbólico) (cosh(t)-1)/t
dt (Integral del coseno hiperbólico)
Shi(x) =   senh(t)/t
dt (Integral del seno hiperbólico) senh(t)/t
dt (Integral del seno hiperbólico)
Erf(x) = 2/PI (1/2)  e
(-t^2) dt = 2/ e
(-t^2) dt = 2/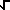 PI PI
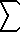 (n=0..inf) (-1) n
x (2n+1) / ( n! (2n+1) ) (Función
de error) (n=0..inf) (-1) n
x (2n+1) / ( n! (2n+1) ) (Función
de error)
FresnelC(x) =   cos(PI/2
t 2) dt cos(PI/2
t 2) dt
FresnelS(x) =   sen(PI/2
t 2) dt sen(PI/2
t 2) dt
dilog(x) =   ln(t)/(1-t)
dt ln(t)/(1-t)
dt
Psi(x) =  ln(Gamma(x)) ln(Gamma(x))
Psi(n,x) = nth derivada de Psi(x)
W(x) = inverso de x*e x
L sub n (x) = (e x/n!)( x n e -x
) (n) (Polinomial de Laguerre, grado n; (n)
significafo nth derivada)
Zeta(s) = 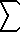 (n=1..inf) 1/n
s (n=1..inf) 1/n
s
Función beta de Dirichlet B(x) = 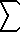 (n=0..inf)
(-1) n / (2n+1) x (n=0..inf)
(-1) n / (2n+1) x
Teoremas con hipertexto tienen pruebas, teoremas relacionados, discusiones,
y/u otra información.
|
|
|


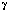 de Euler
= 0.5772156649...
de Euler
= 0.5772156649...