Discussion of
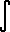 bx dx = bx / ln(b) + C.
bx dx = bx / ln(b) + C.
|
1. Proof
Strategy: Use the 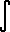 eu du = eu + C
eu du = eu + C
since eln b = b,
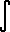 bx dx =
bx dx = 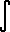 [ (eln b) x ] dx
[ (eln b) x ] dx
= 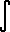 e (ln b) x dx
e (ln b) x dx
set u = (ln b) x
then du = (ln b) dx
substitute...
= 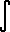 eu (du / ln b)
eu (du / ln b)
= (1 / ln b) 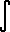 eu du
eu du
solve the integral...
= (1 / ln b) ( eu + C )
= (1 / ln b) eu + C2 (create new constant)
substitute back u = (ln b) x,
= ( 1 / ln b) e(ln b) x + C2
= ( 1 / ln b) ( e(ln b) )x + C2
= ( 1 / ln b) bx + C2
= bx / ln b + C2
Q.E.D.
See also the proof of 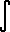 eu du = eu. PROOF
eu du = eu. PROOF
2. You need not memorize
this theorem. Derive it each time you use it.
Consider this example: if you have the integral:
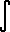 2x dx.
2x dx.
There is no need to memorize the formula. We will get this integral
into the easier form, 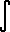 eu
du. eu
du.
Recall that eln(2) = 2
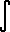 2x dx =
2x dx = 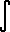 ( eln (2) ) x dx
( eln (2) ) x dx
=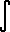 eln (2) x dx
eln (2) x dx
set u = ln(2) x
then du = ln(2) dx
substitute:
= 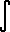 eu (du / ln 2 )
eu (du / ln 2 )
= (1 / ln 2) 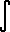 eu
du eu
du
= (1 / ln 2) eu + C
substitute back...
= (1 / ln 2) eln(2) x + C
= (1 / ln 2) ( eln(2) )x + C
= (1 / ln 2) 2x + C ANSWER
This method is actually quite fast; it just looks long because I drew
it out for demonstration purposes.
 |

