Proof: Integral tanh(x)

Home | Teacher | Parents | Glossary | About Us

Email this page to a friend

	Resources
	· Cool Tools · Formulas & Tables · References · Test Preparation · Study Tips · Wonders of Math
	Search

Proof: Integral tanh(x)

(Math | Calculus | Integrals | Table Of | tanh x)

Discussion of (integral)

tanh x dx = ln (cosh x) + C.

1. Proof

Strategy

tanh x =

sinh x

cosh x

(e^x - e^-x) / 2(e^x + ex) / 2

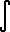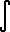tanh x dx = (integral)

e^x - exe^x + ex

set
u = e^x + ex
then we find
du = (e^x - ex) dx

substitute du= (e^x - ex) dx, u = e^x + ex

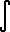= (integral) ^{du

u}

solve

= ln |u| + C

substitute back u = e^x + ex

= ln |e^x + ex| + C

since e^x and ex are always positive

= ln (e^x + ex) + C

since (e^x + ex)/2 = cosh(x)

= ln (2 cosh x) + C
= ln 2 + ln (cosh x) + C

ln 2 is merely a constant that can be combined with C

= ln (cosh x) + C
Q.E.D.