|
|
|

Some of these functions I have seen defined under both intervals (0 to
x) and (x to inf). In that case, both variant definitions
are listed.
gamma = Euler's
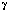 constant
= 0.5772156649... constant
= 0.5772156649...
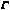 (x) = Gamma(x)
= (x) = Gamma(x)
=   t^(x-1)
e^(-t)dt (Gamma function) t^(x-1)
e^(-t)dt (Gamma function)
B(x,y) =   t^(x-1)
(1-t)^(y-1)DT (Beta function) t^(x-1)
(1-t)^(y-1)DT (Beta function)
Ei(x) =   e^(-t)/t
DT (exponential integral) or it's variant, NONEQUIVALENT
form: e^(-t)/t
DT (exponential integral) or it's variant, NONEQUIVALENT
form:
Ei(x) = 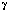 + ln(x) +
+ ln(x) +   (e^t
- 1)/t DT = gamma + ln(x) + (e^t
- 1)/t DT = gamma + ln(x) + 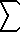 (n=1..inf)x^n/(n*n!) (n=1..inf)x^n/(n*n!)
li(x) =   1/ln(t)
DT (logarithmic integral) 1/ln(t)
DT (logarithmic integral)
Si(x) =   sin(t)/t
DT (sine integral) or it's variant, NONEQUIVALENT
form: sin(t)/t
DT (sine integral) or it's variant, NONEQUIVALENT
form:
Si(x) =   sin(t)/t
DT = PI/2 - sin(t)/t
DT = PI/2 -   sin(t)/t
DT sin(t)/t
DT
Ci(x) =   cos(t)/t
DT (cosine integral) or it's variant, NONEQUIVALENT
form: cos(t)/t
DT (cosine integral) or it's variant, NONEQUIVALENT
form:
CI(x) = -   COs(t)/t
DT = gamma + ln(x) + COs(t)/t
DT = gamma + ln(x) +   (COs(t) - 1) / t DT (cosine integral)
(COs(t) - 1) / t DT (cosine integral)
Chi(x) = gamma + ln(x) +   (cosh(t)-1)/t
DT (hyperbolic cosine integral) (cosh(t)-1)/t
DT (hyperbolic cosine integral)
Shi(x) =   sinh(t)/t
DT (hyperbolic sine integral) sinh(t)/t
DT (hyperbolic sine integral)
Erf(x) = 2/PI^(1/2)  e^(-t^2)
DT = 2/ e^(-t^2)
DT = 2/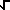 PI PI 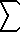 (n=0..inf)
(-1)^n x^(2n+1) / ( n! (2n+1) ) (error
function) (n=0..inf)
(-1)^n x^(2n+1) / ( n! (2n+1) ) (error
function)
FresnelC(x) =   COs(PI/2
t^2) DT COs(PI/2
t^2) DT
FresnelS(x) =   sin(PI/2
t^2) DT sin(PI/2
t^2) DT
dilog(x) =   ln(t)/(1-t)
DT ln(t)/(1-t)
DT
Psi(x) =  ln(Gamma(x)) ln(Gamma(x))
Psi(n,x) = nth derivative of Psi(x)
W(x) = inverse of x*e^x
L sub n (x) = (e^x/n!)( x^n e^(-x)
) (n) (laguerre polynomial degree n. (n)
meaning nth derivative)
Zeta(s) = 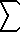 (n=1..inf) 1/n^s (n=1..inf) 1/n^s
Dirichlet's beta function B(x) = 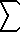 (n=0..inf)
(-1)^n / (2n+1)^x (n=0..inf)
(-1)^n / (2n+1)^x

Theorems with hyperlinks have proofs, related theorems, discussions, and/or
other info.
|
|
|

