|
|
|
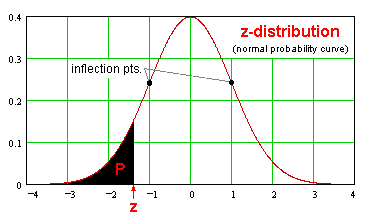
El z- es un N(0, 1) distributión, dando por la ecuación:
f(z) = 1/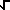 (2PI)
e(-z^2/2) (2PI)
e(-z^2/2)
El área encima de la intervalo (a,b) = normalcdf(a,b) =   e-z^2/2 dz (No es integrable
en forma algebraico.)
e-z^2/2 dz (No es integrable
en forma algebraico.)
La expansión Taylor de lo aribo asiste en (speeding up) la el
cálculo:
normalcdf(-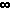 , z) = 1/2
+ 1/ , z) = 1/2
+ 1/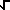 (2PI) (2PI) 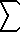 (k=0..
(k=0..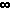 ) [ ( (-1)^k
x^(2k+1) ) / ( (2k+1) 2^k k! ) ] ) [ ( (-1)^k
x^(2k+1) ) / ( (2k+1) 2^k k! ) ]
Probabilidades normal estándar:
(La tabla baja es basando en el área P
debajo de la Curva probabilidad normal estándar, a la izquiera
de la z-estadística respecta.)
| z |
.00 |
.01 |
.02 |
.03 |
.04 |
.05 |
.06 |
.07 |
.08 |
.09 |
| -4.0 |
0.00003 |
0.00003 |
0.00003 |
0.00003 |
0.00003 |
0.00003 |
0.00002 |
0.00002 |
0.00002 |
0.00002 |
| -3.9 |
0.00005 |
0.00005 |
0.00004 |
0.00004 |
0.00004 |
0.00004 |
0.00004 |
0.00004 |
0.00003 |
0.00003 |
| -3.8 |
0.00007 |
0.00007 |
0.00007 |
0.00006 |
0.00006 |
0.00006 |
0.00006 |
0.00005 |
0.00005 |
0.00005 |
| -3.7 |
0.00011 |
0.00010 |
0.00010 |
0.00010 |
0.00009 |
0.00009 |
0.00008 |
0.00008 |
0.00008 |
0.00008 |
| -3.6 |
0.00016 |
0.00015 |
0.00015 |
0.00014 |
0.00014 |
0.00013 |
0.00013 |
0.00012 |
0.00012 |
0.00011 |
| -3.5 |
0.00023 |
0.00022 |
0.00022 |
0.00021 |
0.00020 |
0.00019 |
0.00019 |
0.00018 |
0.00017 |
0.00017 |
| -3.4 |
0.00034 |
0.00032 |
0.00031 |
0.00030 |
0.00029 |
0.00028 |
0.00027 |
0.00026 |
0.00025 |
0.00024 |
| -3.3 |
0.00048 |
0.00047 |
0.00045 |
0.00043 |
0.00042 |
0.00040 |
0.00039 |
0.00038 |
0.00036 |
0.00035 |
| -3.2 |
0.00069 |
0.00066 |
0.00064 |
0.00062 |
0.00060 |
0.00058 |
0.00056 |
0.00054 |
0.00052 |
0.00050 |
| -3.1 |
0.00097 |
0.00094 |
0.00090 |
0.00087 |
0.00084 |
0.00082 |
0.00079 |
0.00076 |
0.00074 |
0.00071 |
| -3.0 |
0.00135 |
0.00131 |
0.00126 |
0.00122 |
0.00118 |
0.00114 |
0.00111 |
0.00107 |
0.00103 |
0.00100 |
| -2.9 |
0.00187 |
0.00181 |
0.00175 |
0.00169 |
0.00164 |
0.00159 |
0.00154 |
0.00149 |
0.00144 |
0.00139 |
| -2.8 |
0.00256 |
0.00248 |
0.00240 |
0.00233 |
0.00226 |
0.00219 |
0.00212 |
0.00205 |
0.00199 |
0.00193 |
| -2.7 |
0.00347 |
0.00336 |
0.00326 |
0.00317 |
0.00307 |
0.00298 |
0.00289 |
0.00280 |
0.00272 |
0.00264 |
| -2.6 |
0.00466 |
0.00453 |
0.00440 |
0.00427 |
0.00415 |
0.00402 |
0.00391 |
0.00379 |
0.00368 |
0.00357 |
| -2.5 |
0.00621 |
0.00604 |
0.00587 |
0.00570 |
0.00554 |
0.00539 |
0.00523 |
0.00508 |
0.00494 |
0.00480 |
| -2.4 |
0.00820 |
0.00798 |
0.00776 |
0.00755 |
0.00734 |
0.00714 |
0.00695 |
0.00676 |
0.00657 |
0.00639 |
| -2.3 |
0.01072 |
0.01044 |
0.01017 |
0.00990 |
0.00964 |
0.00939 |
0.00914 |
0.00889 |
0.00866 |
0.00842 |
| -2.2 |
0.01390 |
0.01355 |
0.01321 |
0.01287 |
0.01255 |
0.01222 |
0.01191 |
0.01160 |
0.01130 |
0.01101 |
| -2.1 |
0.01786 |
0.01743 |
0.01700 |
0.01659 |
0.01618 |
0.01578 |
0.01539 |
0.01500 |
0.01463 |
0.01426 |
| -2.0 |
0.02275 |
0.02222 |
0.02169 |
0.02118 |
0.02067 |
0.02018 |
0.01970 |
0.01923 |
0.01876 |
0.01831 |
| -1.9 |
0.02872 |
0.02807 |
0.02743 |
0.02680 |
0.02619 |
0.02559 |
0.02500 |
0.02442 |
0.02385 |
0.02330 |
| -1.8 |
0.03593 |
0.03515 |
0.03438 |
0.03362 |
0.03288 |
0.03216 |
0.03144 |
0.03074 |
0.03005 |
0.02938 |
| -1.7 |
0.04456 |
0.04363 |
0.04272 |
0.04181 |
0.04093 |
0.04006 |
0.03920 |
0.03836 |
0.03754 |
0.03673 |
| -1.6 |
0.05480 |
0.05370 |
0.05262 |
0.05155 |
0.05050 |
0.04947 |
0.04846 |
0.04746 |
0.04648 |
0.04551 |
| -1.5 |
0.06681 |
0.06552 |
0.06425 |
0.06301 |
0.06178 |
0.06057 |
0.05938 |
0.05821 |
0.05705 |
0.05592 |
| -1.4 |
0.08076 |
0.07927 |
0.07780 |
0.07636 |
0.07493 |
0.07353 |
0.07214 |
0.07078 |
0.06944 |
0.06811 |
| -1.3 |
0.09680 |
0.09510 |
0.09342 |
0.09176 |
0.09012 |
0.08851 |
0.08691 |
0.08534 |
0.08379 |
0.08226 |
| -1.2 |
0.11507 |
0.11314 |
0.11123 |
0.10935 |
0.10749 |
0.10565 |
0.10383 |
0.10204 |
0.10027 |
0.09852 |
| -1.1 |
0.13566 |
0.13350 |
0.13136 |
0.12924 |
0.12714 |
0.12507 |
0.12302 |
0.12100 |
0.11900 |
0.11702 |
| -1.0 |
0.15865 |
0.15625 |
0.15386 |
0.15150 |
0.14917 |
0.14686 |
0.14457 |
0.14231 |
0.14007 |
0.13786 |
| -0.9 |
0.18406 |
0.18141 |
0.17878 |
0.17618 |
0.17361 |
0.17105 |
0.16853 |
0.16602 |
0.16354 |
0.16109 |
| -0.8 |
0.21185 |
0.20897 |
0.20611 |
0.20327 |
0.20045 |
0.19766 |
0.19489 |
0.19215 |
0.18943 |
0.18673 |
| -0.7 |
0.24196 |
0.23885 |
0.23576 |
0.23269 |
0.22965 |
0.22663 |
0.22363 |
0.22065 |
0.21769 |
0.21476 |
| -0.6 |
0.27425 |
0.27093 |
0.26763 |
0.26434 |
0.26108 |
0.25784 |
0.25462 |
0.25143 |
0.24825 |
0.24509 |
| -0.5 |
0.30853 |
0.30502 |
0.30153 |
0.29805 |
0.29460 |
0.29116 |
0.28774 |
0.28434 |
0.28095 |
0.27759 |
| -0.4 |
0.34457 |
0.34090 |
0.33724 |
0.33359 |
0.32997 |
0.32635 |
0.32276 |
0.31917 |
0.31561 |
0.31206 |
| -0.3 |
0.38209 |
0.37828 |
0.37448 |
0.37070 |
0.36692 |
0.36317 |
0.35942 |
0.35569 |
0.35197 |
0.34826 |
| -0.2 |
0.42074 |
0.41683 |
0.41293 |
0.40904 |
0.40516 |
0.40129 |
0.39743 |
0.39358 |
0.38974 |
0.38590 |
| -0.1 |
0.46017 |
0.45620 |
0.45224 |
0.44828 |
0.44433 |
0.44038 |
0.43644 |
0.43250 |
0.42857 |
0.42465 |
| -0.0 |
0.50000 |
0.49601 |
0.49202 |
0.48803 |
0.48404 |
0.48006 |
0.47607 |
0.47209 |
0.46811 |
0.46414 |

|
|
|



 e-z^2/2 dz (No es integrable
en forma algebraico.)
e-z^2/2 dz (No es integrable
en forma algebraico.)