|
|
|
Transformadas del Fourier
 Definiciones
de la transformada del Fourier Definiciones
de la transformada del Fourier
f(x) = 1/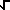 (2 (2 ) )
  g(t) e^(i tx) dt
g(t) e^(i tx) dt
 Identidad inversa
de la transformada del Fourier Identidad inversa
de la transformada del Fourier
g(x) = 1/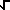 (2 (2 ) )
  f(t) e^(-i tx) dt
f(t) e^(-i tx) dt

Transformadas Fourier seno y coseno
 Definiciones
de las transformadas Definiciones
de las transformadas
f(x) = 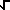 (2/ (2/ ) )
  g(x) cos(xt) dt (Transformada cosena)
g(x) cos(xt) dt (Transformada cosena)
f(x) = 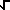 (2/ (2/ ) )
  g(x) sin(xt) dt (Transformada sena)
g(x) sin(xt) dt (Transformada sena)
 Identidades
de las transformadas Identidades
de las transformadas
SI f(x) es par, entonces TransformadaFourierSeno(
TransformadaFourierSeno(f(x)) ) = f(x)
SI f(x) es impar, entonces TransformadaFourierCoseno( TransformadaFourierCoseno(f(x))
) = f(x)
con algunas restricciones de continuidad.

|
|
|


 Definiciones
de la transformada del Fourier
Definiciones
de la transformada del Fourier Identidad inversa
de la transformada del Fourier
Identidad inversa
de la transformada del Fourier Definiciones
de las transformadas
Definiciones
de las transformadas Identidades
de las transformadas
Identidades
de las transformadas