
 |
| Home | Teacher | Parents | Glossary | About Us | |||||||||||
|
|
|||||||||||
|
|
Hyperbolic Definitionssinh(x) = ( e x - e -x )/2csch(x) = 1/sinh(x) = 2/( e x - e -x ) cosh(x) = ( e x + e -x )/2 sech(x) = 1/cosh(x) = 2/( e x + e -x ) tanh(x) = sinh(x)/cosh(x) = ( e x - e -x )/( e x + e -x ) coth(x) = 1/tanh(x) = ( e x + e -x)/( e x - e -x )
cosh 2(x) - sinh 2(x) = 1 tanh 2(x) + sech 2(x) = 1 coth 2(x) - csch 2(x) = 1
Inverse Hyperbolic Definitionsarcsinh(z) = ln( z +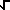 (z
2 + 1) ) (z
2 + 1) )
arccosh(z) = ln( z arctanh(z) = 1/2 ln( (1+z)/(1-z) ) arccsch(z) = ln( (1+ arcsech(z) = ln( (1 arccoth(z) = 1/2 ln( (z+1)/(z-1) )
Relations to Trigonometric Functionssinh(z) = -i sin(iz)csch(z) = i csc(iz) cosh(z) = cos(iz) sech(z) = sec(iz) tanh(z) = -i tan(iz) coth(z) = i cot(iz)
|
|
||||||||||||||||
|
|