|
|
|
 |
 |
 |
 |
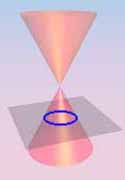
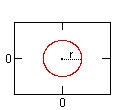
Círculo
 |
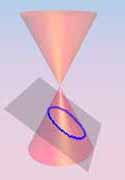
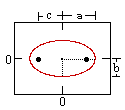
Elipse (h)
 |
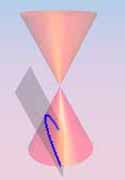
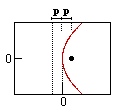
Parábola (h)
 |
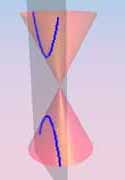
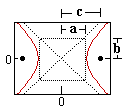
Hipérbola (h)
 |
Definición:
Una sección cónica es la intersección de un plano
y un cono. |
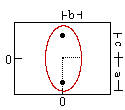
Elipse (v)
 |
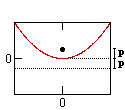
Parábola (v)
 |
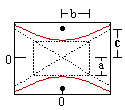
Hipérbola (v)
 |
Cambiando el ángulo y el lugar de la intersección, podemos
crear un círculo, un elipse, una parábola o una hipérbola;
o en el caso especial cuando el plano se pone en contacto con el vértice:
un punto, una línea o 2 líneas intersectadas.
La ecuación general de una sección
cónica:
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 |
El tipo de sección puede ser descubierta
por el signo de: B2 - 4AC
| Si B2 - 4AC es... |
pues la curva es...
|
| < 0 |
un elipse, un círculo, un punto o ninguna curva.
|
| = 0 |
una parábola, 2 líneas paralelas, 1 línea o
ninguna curva.
|
| > 0 |
una hipérbola o 2 líneas intersectadas.
|
Las secciones cónicas. Para, en cada uno de los abajo
mencionados casos, lograr un centro (j, k) en vez de (0, 0), reponga cada
término x con un (x-j) y cada témino y con
un (y-k).
| |
Círculo |
Elipse |
Parábola |
Hipérbola |
| Ecuación (vértice horizontal): |
x2 + y2 = r2 |
x2 / a2 + y2 / b2 =
1 |
4px = y2 |
x2 / a2 - y2 / b2 =
1 |
| Ecuaciones de las asíntotas: |
|
|
|
y = ± (b/a)x |
| Ecuación (vértice vertical): |
x2 + y2 = r2 |
y2 / a2 + x2 / b2 =
1 |
4py = x2 |
y2 / a2 - x2 / b2 =
1 |
| Ecuaciones de las asíntotas: |
|
|
|
x = ± (b/a)y |
| Variables: |
r = el radio del círculo |
a = el radio mayor (= 1/2 la longitud del eje mayor)
b = el radio menor (= 1/2 la longitud del eje menor)
c = la distancia desde el centre al foco |
p = la distancia desde el vértice al foco (o a la
directriz) |
a = 1/2 la longitud del eje mayor
b = 1/2 la longitud del eje menor
c = la distancia desde el centro al foco |
| Excentricidad: |
0 |
|
c/a |
c/a |
| El relación al foco: |
p = 0 |
a2 - b2 = c2 |
p = p |
a2 + b2 = c2 |
| Definición: es el conjunto de todos los puntos que cumple
la condición... |
la distancia al origen es constante |
la suma del las distancias a cada foco es constante |
la distancia al foco = la distancia a la directriz |
la diferencia entre las distancias a cada foco es constante |
| Tópicos similares: |
La sección geométrica
sobre círculos |
|
|
|
|
|
|

